Último teorema de Fermat
 Resulta curioso cómo la mayoría de los teoremas propuestos por matemáticos clásicos han sido demostrados en un breve período de tiempo mientras que otros permanecen "estrujando los sesos" a los más doctos en la materia hasta que lo consiguen.
Resulta curioso cómo la mayoría de los teoremas propuestos por matemáticos clásicos han sido demostrados en un breve período de tiempo mientras que otros permanecen "estrujando los sesos" a los más doctos en la materia hasta que lo consiguen.
En el caso que nos ocupa hablamos del francés Pierre de Fermat cuya vida contribuyó a sentar las bases del cálculo moderno.
Al final de su vida dejó a pie de página de uno de sus libros una de las notas más famosas de esta disciplina y que trajo de cabeza a muchos matemáticos de la época (s. XVII):
"Es imposible encontrar la forma de convertir un cubo en la suma de dos cubos, una potencia cuarta en la suma de dos potencias cuartas, o en general cualquier potencia más alta que el cuadrado en la suma de dos potencias de la misma clase; para este hecho he encontrado una demostración excelente. El espacio del papel es demasiado pequeño para que la demostración quepa en él."
Lo que nos viene a decir:
Los más desconfiados aseguraban que ese achaco a la falta de espacio para no demostrarlo es una prueba inequívoca de que realmente Fermat no sabía resolverlo. De hecho, fueron necesarios 325 años para que alguien diera una demostración. Sí señores! hace 14 años por fin parecía que las 100 páginas del inglés Andrew Wiles nos habían sacado del atolladero, sin embargo en la primera edición había un importante fallo. Por lo que no fue aceptada por la comunidad científica hasta que se solucionara completamente.Si n es un número entero mayor que 2 (o sea, n > 2), entonces no existen números enteros a, b y c distintos de 0, tales que cumplan la igualdad:
Obviamente no vamos a poner aquí esta demostración, pero sí comentar que resulta curioso que Wilesnos utilizara para su demostración técnicas matemáticas desarrolladas posteriormente a la muerte de Fermat. O incluso el hecho de haber necesitado 100 páginas para demostrar algo que según el matemático francés parecía poder hacer en unas pocas líneas, según deducimos de la nota.
Fuentes: Wikipedia.
De lo que hablamos
Previously on G'n R
-
►
2010
(111)
- ► septiembre (15)
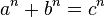






2 comentarios:
5bftnhrtyj
Gran comentario
Publicar un comentario